Bias Variance Tradeoff

To start of with,
Bias is an error introduced in the model due to the oversimplification of the algorithm used(which means it doesn’t fit the data properly) which is also called as underfitting. Imagine fitting a linear regression to a dataset that has a non-linear pattern, No matter how many more observations you collect, a linear regression won’t be able to model the curves in that data! This is known as under-fitting.

Variance is error introduced in the model due to a too complex algorithm, which means the model basically remembers the training data and produces lower error while training but fails in test dataset. which is also termed as overfitting.


Let’s go through complexity of the model.


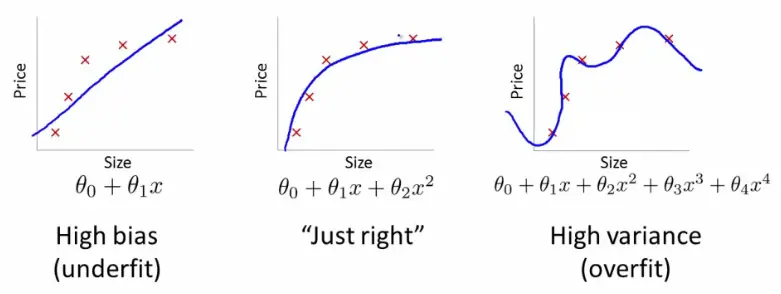Figure 1. endtoend.ai


Say, the complexity of the model is defined by degree of polynomial. now, you fit a model with degree of polynomial ‘d’ and get some estimates of how well your fitted hypothesis will generalise to new examples. In the above image you can interpret how well various degrees of polynomials fits to the data, i.e the increase in complexity of the model increases variance in the model(overfitting).

Now, how do you choose right degree of polynomial for your dataset, one potential method you can follow is cross validation.

Now that we have two kinds of error we define the right degree of polynomial by cross validations error and trian error. we never choose test error as a choice of defining a model performance or parameter tuning.

The following graph shows the bias variance tradeoff considering degree of polynomail (model complexity) and error on cross validation and train data.



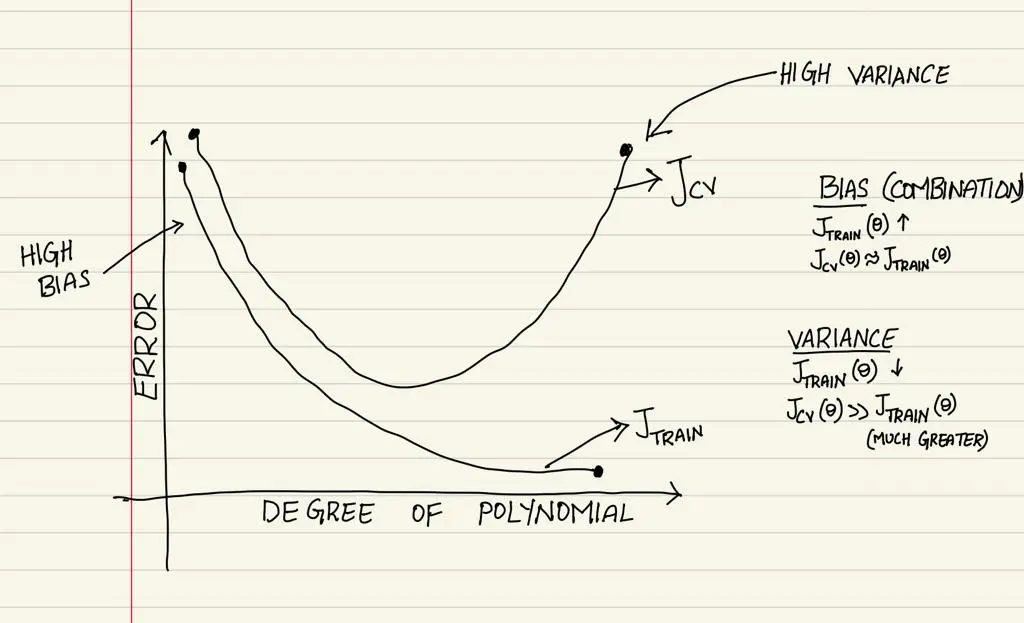
Refer to the bias and variance combination of validation and train error from the image. As the degree of polynomial increases the model tends to remember the data thus training have low error, but in cross validation the model performs poor. you need to select a degree of polynomial where both bias and variance are low. Hence, the name TRADEOFF.

The other important method often used in conventional machine learning to tackle bias variance tradeoff is by using REGULARIZATION.

I will not got into nuts and bolts of regularization, but we will see the effect of regularization parameter in overfitting of data.

Lets consider L2 regularization.



As our objective is to minimize the loss function in any setting, The decrease in lambda values should increase the values of Theta, as the overall loss should be decreased. that means the values of theta are still higher which means the model have high variance(overfitting). Remember that higher values of theta is same as higher value of degree of polynomial.



As previously said, even here we consider a sweet spot for the lambda value using cross validation error to balance bias and variance. There is no escaping the relationship between bias and variance in machine learning. Increasing the bias will decrease the variance. Increasing the variance will decrease bias.


Some tips if your model isnt working:

  • Get more training data - fix high variance problem
  • If your hypothesis already suffering from high bias, getting more data doesn’t solve the problem.
  • Try smaller set of features - fixes high variance problem
  • Try getting additions features(feature engineering) - fixes high bias problem
  • Try adding polynomial features - fixes high bias problem
  • Try decreasing or increasing learning rate and regularization parameters.


USEFUL FINDINGS: (from external source)

  1. The k-nearest neighbor algorithm has low bias and high variance, but the trade-off can be changed by increasing the value of k which increases the number of neighbors that contribute to the prediction and in turn increases the bias of the model.
  2. The support vector machine algorithm has low bias and high variance, but the trade-off can be changed by increasing the C parameter that influences the number of violations of the margin allowed in the training data which increases the bias but decreases the variance.
  3. The decision tree has low bias and high variance, you can decrease the depth of the tree or use fewer attributes.
  4. The linear regression has low variance and high bias, you can increase the number of features or use another regression that better fits the data.

Best!
Siddhartha Putti
putti.s@northeastern.edu