A Complete Record of Jack and Ashley’s Last Peaceful Talk
Jack just finished a phone call with Paul Bettany.
Ashley: Eigen, eigen… Pee-see-ay… I never knew you speak any German besides, you know, bier.
Jack: Calm down. It’s just that Paul has been reading a lot of math, God knows how Jennifer are obsessed with mathematician.
Ashley: Oh really, tell me more about it! You know I’ve got an audition next week right? For “Algebra Man: Curse of Dimensionality”.
Jack: Ah, Principal Component Analysis or PCA, it’s just a method of summarizing some data. Look, we have some glasses of whisky on the table, and of course we can describe each whisky by its colour, age, taste etc., then we can compose a 4 pages’ appreciation paper for each of it. But no, this is just way too much for those whisky newbies! So, instead of a long list of Whisky features, we can use PCA to summarize each whisky through extracting the maximum possible information from the drink while reducing the noise and ignoring the redundant information.
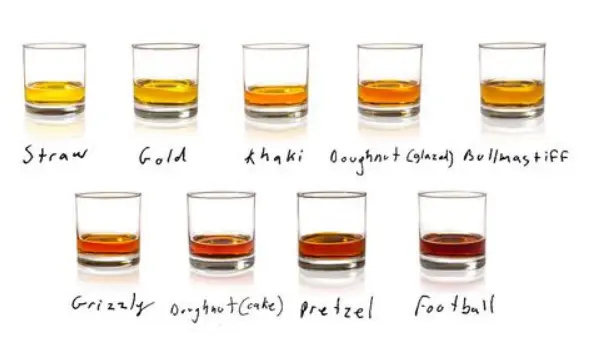
(The Esquire Rainbow of Whiskey)
Ashley: Hmm, okay. Does it mean PCA returns you a new whisky color or taste that helps you know this drink better?
Jack: Not exactly, the best part of PCA is that it doesn’t restrict itself to currently existing variables! Instead, it creates new variables when extra expression is needed, which is, the Principal Components (PC). PC are constructed as linear combinations or mixtures of the initial variables. These combinations are done in such a way that the PCs are uncorrelated and most of the information within the initial variables is squeezed like lime into the first PC~ Like when you have the first sip, you get most of the taste, juicy!
Ashley: Interesting. But I still doubt how PCA distills the drink… I mean, summarizes the information for you? How does it know what’s important and what isn’t?
Jack: Good question. Perhaps I should make a little drawing (takes a napkin and starts scribbling).
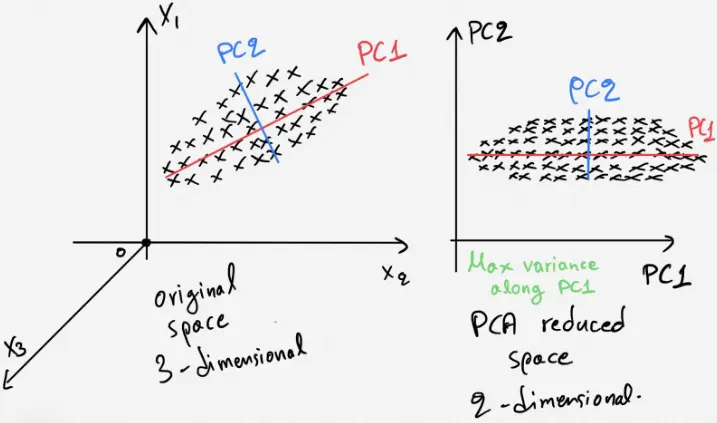
Then Johnny used his wind borrowed from the Charlie movie, the black line starts to spin.
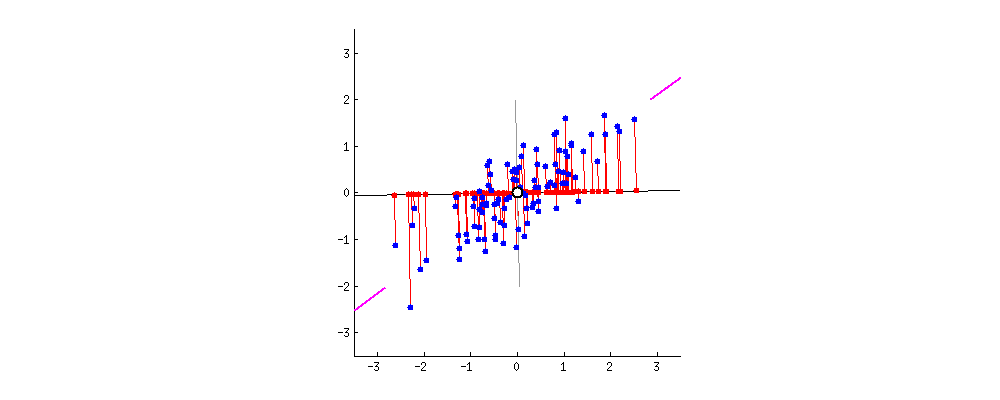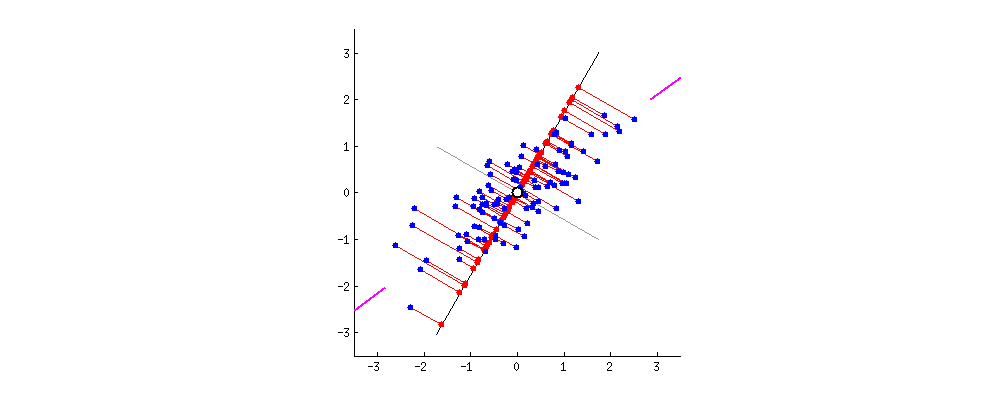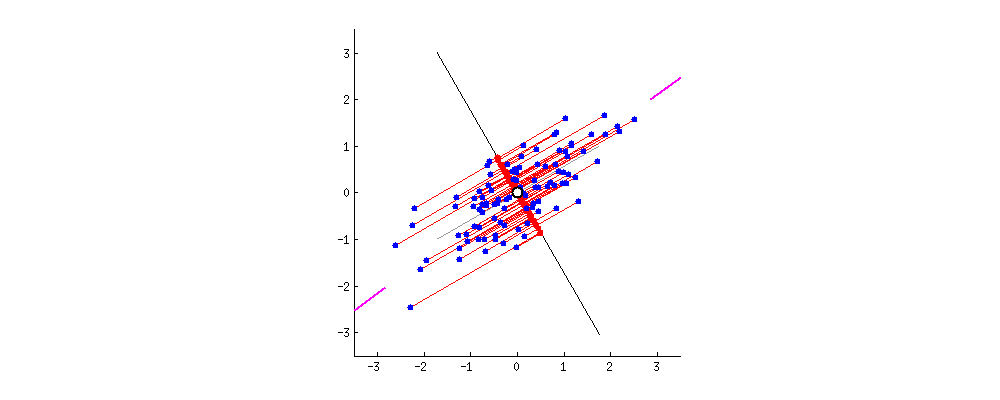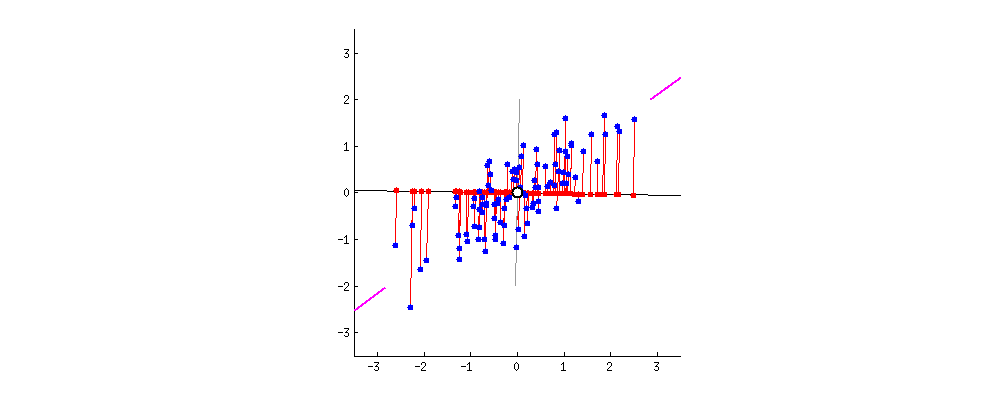
Johnny’s dog: Magical, papa! I think I can see why the two goals yield the same result. And I also Ashley that you mentioned eigenvectors and eigenvalues, how are they related to PCA?
Jack: My sweetheart, let me explain to you! Eigenvalues and eigenvectors are the results of eigen-decomposition of matrix. The decomposition can be derived from the fundamental property of eigenvectors:
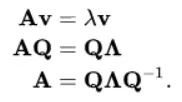
The 2 × 2 real matrix A, may be decomposed into a diagonal matrix through
multiplication of a non-singular matrix B
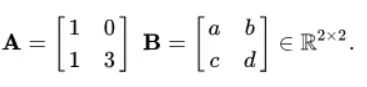
Then
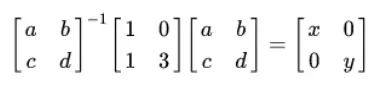for some real diagonal matrix
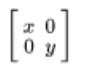
Multiplying both sides of the equation on the left by B:
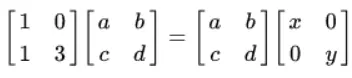
Jack’s dog: Oh I see! The above equation can be decomposed into two simultaneous equations:
Letting
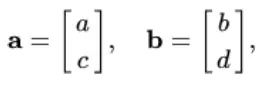
this gives us two vector equations:
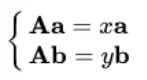
And can be represented by a single vector equation involving two solutions as eigenvalues:
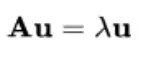where λ represents the two
eigenvalues x and y, and u represents the vectors a and b.
Shifting λu to the left-hand side and factoring u out
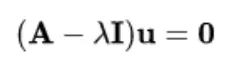
Since B is non-singular, it is essential that u is nonzero. Therefore,
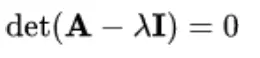
Thus
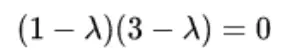
giving us the solutions of the eigenvalues for the matrix A as λ = 1 or λ = 3.
And the resulting diagonal matrix from the eigen-decomposition of A is thus
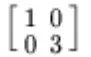
Jack: Absolutely! Putting the solutions back into the above simultaneous equations
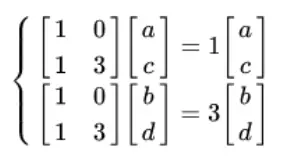
Solving the equations, we have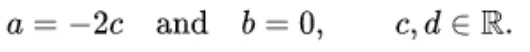 
Thus, the matrix B required for the eigen-decomposition of A is
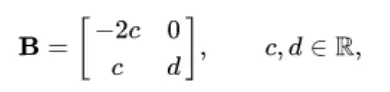
that is:
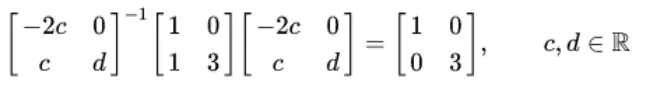
Ashley: Zzzzz…. Oh! Darling, what should I say? You just keep surprising me every day! Now give me a example of PCA that happened to you.
Jack: There was one. Vinona…
Ashley: Your silly tattoo?
Jack: Say that again?!